| ねこぱぱ問題に挑戦! |
|---|
| 大学入試問題(数学) |
第9話 行列のできるうまい店!
|
●行列ができるほど美味しいと評判の店 ある町に、美味しいと評判の2軒の中華料理屋さんがありました。 一軒の店の名は「ねこ飯店」、もう一軒は「ぱぱ来軒」といいました。 2軒とも大変美味しいと評判でしたので、この町の人たちはどちらのお店で 食事をしようかといつも悩んでいました。 (みなさんの近所にもこんな店ありませんか?あったら教えて下さいね!) さて、この2軒の一番の自慢はラーメンとチャーハンでしたが、値段は次の ように微妙にちがっていました。
みなさんのまわりにも、このように表にすると分かりやすいものがたくさん ありますよね。 例えば、A君とB君の数学と英語の点数を表にすると次の様になりますね。
数学の世界でも、このような数字の集まりを扱うことがあります。 でも、いちいち表にしていたのでは肝心の計算がはかどりませんので、 次のように( )カッコを使って表すことにしています。 
このような表し方を『行列』といいます。 今回はこの『行列』について少し勉強してみましょう。 ●『行列』の計算は簡単です。「和」と「差」 先ほどのA君とB君のテストの点数の表を思い出して下さい。 この点数は2学期中間テストの点数だったとします。 この2人、実はライバルだったのです。 2人とも英語と数学が大得意科目でしたので、それぞれの科目について中間 テストと期末テストの合計点で勝負をしていました。 先ほどの中間テストは次のような点数でしたね。
そして、12月のある日、期末テストの結果が返ってきました。
各科目ごとに合計点を出すには、表の同じ場所の点数を足し算しますね。
この表から分かるように、今回は1勝1敗で引き分けとなりました。 行列の「足し算」や「引き算」はこれと全く同じように、同じ場所どうしを 足し算したり、引き算したりします。 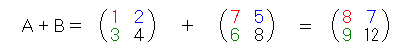
●『行列』の「実数倍」 さてさて、実はA君とB君は双子の兄弟だったのです。 2人は数学と英語の合計点に100をかけた金額のお年玉を、今度のお正月 におじいちゃんとおばあちゃんからもらえる約束になっていたそうです。 今回この2人はそれぞれいくらもらえるかと言うと・・・ 先ほどの合計点の表の数字を全部100倍すればOKですね。
ちょっともらい過ぎですかねぇ?! 行列の計算にもこれと同じように、全ての数を何倍かすることがあります。 
●『行列』のかけ算はちょっとややこしいぞ!! 以上の計算は、小学校3、4年生でもできてしまうと思います。 ところが、『行列』のかけ算はちょっと計算のパターンが難しくなります。 といっても少し練習をすれば、すぐにできるようになりますよ。 まず、先ほどの「ねこ飯店」と「ぱぱ来軒」の値段を思い出して下さい。
さて、この2つのお店でそれぞれ ラーメンを4杯、チャーハンを6杯 注文したとします。それぞれのお店でいくら払うか計算してみますね。 ねこ飯店 ・・ 550×4 + 700×6 = 6400(円) ぱぱ来軒 ・・ 600×4 + 650×6 = 6300(円) この計算を『行列』では、次の様に表します。 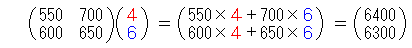
●この計算を更にパワーアップすると・・ このかけ算の計算を発展させて、次のような計算を行います。 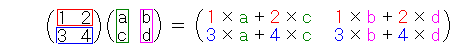
先ほどの計算を、2組分一度に計算していることが分かりますか? ●ここでちょっと計算の練習をしてみましょう。 A=  、B= 、B=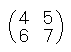 のとき、次を計算してみて下さい。 のとき、次を計算してみて下さい。(1) AB=  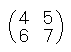 (2) BA= 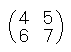  答えは・・ (1) 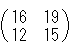 (2) (2)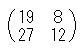 となります。 となります。ここでちょっと考えて下さいね。 普通かけ算は、かける順番を変えても、計算の結果は変わりませんでしたね。 例) 2×3=6 3×2=6 ところが、『行列』のかけ算の場合は計算が複雑になるため、かける順番を 変えると計算の結果が違ってきます! 絶対に違う結果になるかというと、中には一緒になるものもあります。 しかし、普通は(難しい言葉で「一般的には」といいます。)かける順番を 変えると、その計算結果は違ってきます。 ●教訓 『行列』のかけ算では、一般的に AB=BA とはなりません。 中学生のみなさんは という公式を習ったと思います。 この公式も『行列』の場合は(一般に)使えません。 なぜかと言うと、公式を作る途中で AB=BA を使っているからです。 『行列』について勉強していくと、もっといろいろな面白い性質があるのですが、 今回はこのあたりにしておきます。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
それでは、がんばって大学入試問題に挑戦してみましょう! ここをクリックしてね。 |
|---|