ねこぱぱ問題に挑戦！
中学生にも解ける！
大学入試問題（数学）

第１０話　『行列』君のすごい技（わざ）！

●これが「ねこぱぱ」マークです！ 　突然ですが、これが「ねこぱぱマーク」です。 　どこかで見かけたら、思い出して下さいね！ ∧∧ ＝　＝ 　 ∧∧ ＞　＜ ●行列のかけ算（第９問）を思い出してみましょう 　第９問では行列の計算を勉強しましたが、覚えていてくれるでしょうか？？ 　今回は「行列のかけ算」が中心となりますので、思い出してみましょう・・ 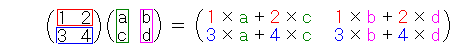　っていうのを思い出して下さいね。今回はこれだけでＯＫです。 　忘れちゃった人は、こちら（第９問）をもう一度おさらいしてみてね。 ●行列で「ねこぱぱマーク」を変換してみよう！ 　さて、先ほどの「ねこぱぱマーク」を、行列のかけ算で移動してみましょう。 　まず、方眼紙に、次の点を結んで「ねこぱぱマーク」を描いてみて下さい。 　　　左のみみ　（２、５）→（３、７）→（４、５） 　　　右のみみ　（５、５）→（６、７）→（７、５） 　　　左のひげ　（１、２）→（３、３）→（１、４） 　　　右のひげ　（８、２）→（６、３）→（８、４） 　下の図のような、「ねこぱぱマーク」が描けると思います。 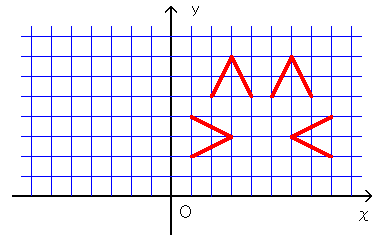　　　　 　さて、この図を描いた１２個の点を、次の行列で移動してみましょう。 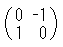　　　 　例えば、一番最初の（２、４）という点は・・ 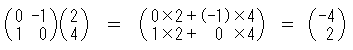　　　 　という計算から、（−４、２）という点に移ることにするわけです。 　いくつか計算すると、どのように移す計算かわかるかもしれませんが、 　新しい「ねこぱぱマーク」は、次のような点で描かれることになります。 　　　左のみみ　（−５、２）→（−７、３）→（−５、４） 　　　右のみみ　（−５、５）→（−７、６）→（−７、７） 　　　左のひげ　（−２、１）→（−３、３）→（−４、１） 　　　右のひげ　（−２、８）→（−３、６）→（−４、８） 　これを先ほどの「ねこぱぱマーク」と同じ方眼紙に描いてみると・・ 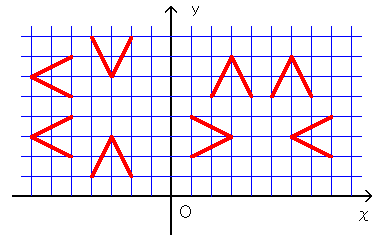　　　　 　「ねこぱぱマーク」が横を向いて寝てしまいましたね！　 ●行列による『一次変換』って言いますが・・ 　ちょっと用語が難しくなりますが、この様に、ある点を行列のかけ算を 　利用して別の点に移すことを、行列による『一次変換』と言います。　 　少し前までは高校の数学でもこの『一次変換』を習っていたのですが、 　１９９４年からはカリキュラム（高校で勉強する内容）が変わった時に 　消えてしまいました・・・ 　理系の大学や、文系も経済学部などへ進むと『一次変換』を習います。 　『行列』を変えれば「ねこぱぱマーク」もいろいろな形に変わります。 　面白い変換の行列が見つかったら、ねこぱぱにも教えて下さいね！！

それでは、がんばって大学入試問題に挑戦してみましょう！ ここをクリックしてね。