ねこぱぱ問題に挑戦！
中学生にも解ける！
大学入試問題（数学）

第６話　「ぬり絵」問題　第２弾！！

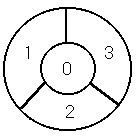
●こんどの塗り絵はちょっと手強いぞ！ 　今回は前回に引き続き、塗り絵の問題です。 　ちょっとパワーアップしているので、がんばって考えてみてね！ 　まずルールを確認しておきましょう。 　 　（ルール） 　　１　■赤■、■青■、■黄■、■紫■　の４色で地図に色を付けていきます。 　　２　４色全部使って下さい。 　　３　隣り合う領土は、異なった色で塗って下さい。 　　４　図形はこのままの位置で固定します。（くるくる回してはいけません。） ●まず、この図形はどうでしょう？ 　使う色が４色で、塗る場所が４カ所ありますから、一つの色は１回しか使えませんね。 　まず真ん中から塗っていきましょう。（これが今回の問題のポイントです。） 　（１）　真ん中は４色のうち、どの色を塗ってもＯＫですから　・・・　４通り　 　（２）　１番は残り３色のどれかを塗りますから　　　　　　　・・・　３通り　 　（３）　２番はまだ使っていない２色のどちらかですから　　　・・・　２通り　 　（４）　３番は最後に残った色を塗りますね。　　　　　　　　・・・　１通り　 　以上のことから、塗り方は全部で・・ 　　　４×３×２×１＝２４（通り） 　となります。 　前回（第５問）を解いてくれた人は、多分楽勝ですよね！？・・・ ●今度はちょっぴり、ややこしいかも・・・ 　今度は、円の外側を４つに分けた図で考えてみましょう。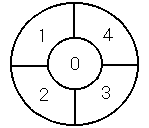 　（１）　やっぱり真ん中から塗ってみましょう。０番は　　　　・・・　４通り 　（２）　１番も０番以外の３通りありますよね！　　　　　　　・・・　３通り 　ここまでで、　４×３＝１２（通り）　の塗り方があります。 　この後、２、３、４番の塗り方が何通りあるかわかれば、解決ですよね。 　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 　　例として、０番に■紫■、１番に■赤■を塗った場合で考えてみましょう。 　　◎混乱しそうな人は、自分で図を描いて実際に塗っていってみて下さいね。 　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 　（３）　２番は、０番（紫）１番（赤）以外の色を塗りますから・・・　２通り 　　　　　（■青■を塗ったとします。） 　（４）　３番は、０番（紫）と２番（青）と隣り合っています 　　　　　から、赤か黄を塗らなくてはなりませんね。　　　　　・・・　２通り 　　　　　（■赤■を塗ったとします。） 　（５）　４番は、０番（紫）、１番（赤）、３番（赤） 　　　　　と異なった色（青か黄）で塗らなくてはなりません。　・・・　２通り 　　　　　（■青■を塗ったとします。） 　従って、（３）×（４）×（５）＝８（通り）　！？ 　んっ！？　　引っかからずに気がついたかな？？？？ 　最後の（５）で青を塗った場合はダメですよ。 　だって黄色を使ってないじゃないですか！！！ ●可能性のある塗り方を全て書き出してみましょう。 　そこで、先ほどの（３）（４）（５）に従って、可能性のある塗り方を全て書き出して 　表にしてみることにします。　（０番は紫で、１番は赤でしたね。） 　Ｎｏ　 　１番　 　２番　 　３番　 　４番　 　判定　 　　１　 　■赤■　 　■青■　 　■赤■　 　■青■　 　×１　 　　２　 　■赤■　 　■青■　 　■赤■　 　■黄■　 　◎　 　　３　 　■赤■　 　■青■　 　■黄■　 　■赤■　 　×２　 　　４　 　■赤■　 　■青■　 　■黄■　 　■青■　 　◎　　 　　５　 　■赤■　 　■黄■　 　■赤■　 　■青■　 　◎　　 　　６　 　■赤■　 　■黄■　 　■赤■　 　■黄■　 　×１　 　　７　 　■赤■　 　■黄■　 　■青■　 　■赤■　 　×２　 　　８　 　■赤■　 　■黄■　 　■青■　 　■黄■　 　◎　　 　　　　×１　・・・　４色使っていないので、ダメ！ 　　　　×２　・・・　１番と４番が同じ色になってしまうので、ダメ！ 　ということで、（３）（４）（５）の塗り方は、４通りあることが分かります。 　従って、２番目の図形を塗り分ける方法は全部で、 　　　（０番の塗り方）×（１番の塗り方）×（２・３・４番の塗り方） 　　＝　４（通り）×　　　３（通り）×　　　４（通り） 　　＝　４８（通り） 　あることになります。 ●教訓　ややこしい時は、まず全部書いてみて、後でダメなものを除いていく 　この方法は、意見面倒くさいようですが、とりあえず全て書き出して、後で 　ダメなものを除いていく方法も、問題を解く時の、大切な戦略のひとつです。 ●表にするのが面倒くさい人は、こんな方法もあります。 　上ような表を作る以外にも、考えられるパターンを全て書き出す方法には、 　このほかに、下の図のように「枝分かれ」のような図を書く方法もあります。 　　　　　１番　・・・　　　　　　　　　■■　赤　■■　　　　　　　　　 　　　　　　　　　　　　　　　　　　／　　　　　　　　　＼　　　　　　　 　　　　　２番　・・・　　　　　　青　　　　　　　　　　　黄　　　　　　 　　　　　　　　　　　　　　　／　　　＼　　　　　　　／　　　＼　　　　 　　　　　３番　・・・　　　赤　　　　　黄　　　　　赤　　　　　青　　　 　　　　　　　　　　　　　／　＼　　　／　＼　　　／　＼　　　／　＼　　 　　　　　４番　・・・　青　　　黄　赤　　　青　青　　　黄　赤　　　黄　 　　　　　Ｎｏ　・・・　１　　　２　３　　　４　５　　　６　７　　　８　 　　　　　判定　・・・　×　　　◎　×　　　◎　◎　　　×　×　　　◎　 　この図のことを「樹形図（じゅけいず）」といいます。（木の形に似てるでしょ？）

それでは、がんばって大学入試問題に挑戦してみましょう！ ここをクリックしてね。