| ねこぱぱ問題に挑戦! |
|---|
| 大学入試問題(数学) |
第8話 どこまでも真っ直ぐなヤツ、彼の名は「直線」!
|
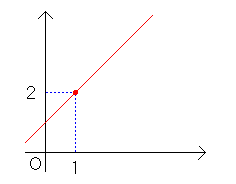
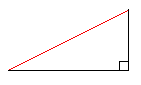
●今、明かされる「直線」君の全て!? 直線君ってどんなヤツ? さて前回は、直線について少しお話しましたが、今回はその直線君についてもう少し 詳しく調べてみることにしましょう。 直線の方程式を確認しておきますね。 y=aχ+b【a】のことを【傾き】といい、【b】のことを【y切片】といいましたね。 まず、直線の方程式を求めることからおさらいしておきましょう。 ●「傾き」と「通る点」で方程式は決まります。 もし、あなたが中学生でしたら、直線の方程式を求めるには「傾き」と「y切片」 が必要であることをもう習ったでしょうか? あなたが高校生以上の方でしたら、 「y切片じゃなくても、どこか一つ通る点が分かれば方程式なんて楽勝じゃん!」 と言うと思います。 このページは、中学生の人を主な対象に作っていますが、今回は特別に秘密の公式 を公開?しておきましょう。 ●点A(1、2)を通り、傾き1の直線の方程式 今ここに下の図のような点A(1、2)を通り、傾き1の直線があったとします。
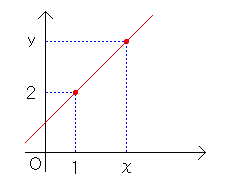
y切片はすぐに分かってしまうのですが、ここではちょっと我慢して、次のような 考え方で直線の方程式を求めてみます。 この直線上に、もう1つ点P(χ、y)をあなたの好きな所にとってみて下さい。 今回は説明の都合上、下のような場所に点Pをとってみますが、もっと右上の方が 好きな人はそちらでもOKですし、反対に左下が好きな人はそちらでもOKです。
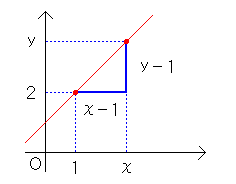
さて、この二つの点、点Aと点Pの間にはある関係が必ず成り立っています。 あなたはそれが分かりますか?? 点Pがもっと右上でも、左上でも必ず成り立つ関係ですよ・・・ それは、点Aと点Pとの傾きが必ず1になるということです。 「なぁーんだ、当たり前じゃん」と思った人は、次の計算は大丈夫ですか? 点A(1、2) と 点P(χ、y) との傾きを計算すると・・・
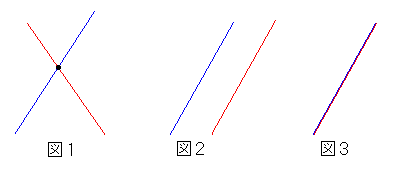
y−2 (傾き)= ───── χ−1 傾きは1ですから、 y−2 ───── = 1 χ−1 この式を地道に変形していくと・・・ y−2 = 1・(χ−1) y−2 = χ−1 ∴ y = χ+1 少し難しい話になるかもしれませんが、直線の方程式というのは・・ 【直線上のどの点についても成り立つ式】ですね。 今求めた式は、点Pが直線上にある限り必ず成り立ちますから、y=χ+1 で、 直線の方程式の完成です! (TV「チューボーですよ」風に・・・見てます?) ●点A(a、b)を通り、傾きmの直線の方程式 今と同じようにして、直線の方程式を求める新しい公式を作ってみます。 点P(a,b)を通り、傾きmの直線の方程式を作ります。 y−b ───── = m より x−a ┌────────────────────────────────────┐ │公式 │ │ │ │ 点A(a、b)を通り、傾きmの直線の方程式は y−b=m(x−a) │ └────────────────────────────────────┘ ●二人の「直線」君の関係は?? 次に、直線君と直線さんの二人がいた場合を考えてみましょう。 直線A君 ・・ y=ax+b 直線Bさん ・・ y=cx+d とし、この二人の関係を調べてみましょう。 多くの場合、この二人は図1のように1点で交わっていますね。 長い人生、一度だけどこかで出会えるわけです。 ところが、傾きが同じになった場合この二人は一生出会うことなく終わってしまい ますね。(図2) ところがところが、y切片であるbとdまでが一致してしまうと、二人は全く同じ 直線となり、一生くっついたまま過ごします。(図3)
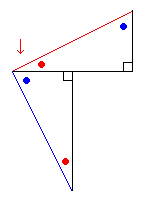
直線A君と直線Bさんの人生はこの3通りしかありません。 あなたならどの人生がいいですか? ●直線が垂直に交わるには・・ さて、上の3つの関係の中で一番多い関係は1番目の「1点で交わる」場合です。 その中で一番激しく(?)交わっている「垂直に交わる」場合を考えてみます。 1 直線A君の傾きが ─ であったとき、直線Bさんは傾きをいくつにすれば垂直に 2 交わることができるでしょうか? いろいろな説明の仕方があるのですが、今回は三角形を利用して説明してみます。 傾きが1/2ということは、右へ2つ進むと、上に1つ上がるということですね。 このことを元に、底辺の長さが2、高さが1の図のような直角三角形を書きます。
一つの三角形を回転したのですから、二つの三角形は同じ三角形ですね。 これを、「二つの三角形は合同である。」といいます。
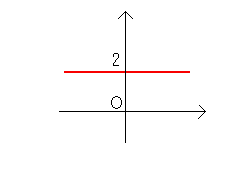
90度になることはOKでしょうか? ● + ● = 90(度) すると、下につけた三角形も同じ(合同な)三角形ですから、赤丸●と青丸●では 同じように90度になりますね。 そこで、図の中の赤い矢印↓の部分に注目してみて下さい。 上の三角形の赤丸●と下の三角形の青丸●が合わさっていますから、ここも90度 になりますね。 ということは・・ 上の三角形の赤線と下の三角形の青線は垂直に交わっていることになりますね。 下の三角形は、1つ進んで、2つ下がっていますから青線の傾きは −2 となります。 同じように考えていくと・・ 1 傾き3 に垂直な傾きは −─ 3 2 3 傾きが ─ の場合、垂直な傾きは −─ となります。 3 2 自分で図を描いて確認してみて下さいね。 簡単に言うと、元の傾きをひっくり返してマイナス(−)をつければ垂直な傾き ができるのですが、高校ではもう少しカッコよく次のような言葉で習います。 ┌────────────────────────────────────┐ │重要 │ │ │ │ 傾きm と 傾きm’ とが垂直になる条件は m×m’=−1 │ └────────────────────────────────────┘ 垂直になる二つの傾きをかけ算してみて下さい。みんな−1になりますよね。 ●直線君の仲間のちょっと個性的なヤツ みなさんのお友だちの中にも、ちょっと個性的な人が何人かいると思います。 それと同じように直線君の仲間にも、ちょっと変わった仲間が二人います。 一人は真横の直線君で、もう一人は縦の直線君です。 真横の直線君は、傾きが0の場合ですでの、y=ax+b のaが0となり、 y=b という形で表されます。 例えば、左の図の直線の方程式は y=2 と表されます。
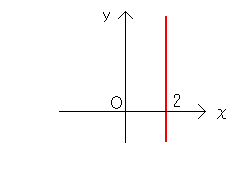
この直線上の点の座標をいくつか書いてみると・・ (2、0)(2、1)(2、2)(2、3)(2、4)・・ となり、x座標はずーっと2のままですね。それで、縦の直線の方程式は x=2 という式で表されます。 今回は少し数学らしい?お話になってしまいましたが、いかがだったでしょうか? |
|
それでは、がんばって大学入試問題に挑戦してみましょう! ここをクリックしてね。 |
|---|