ねこぱぱ問題に挑戦！
中学生にも解ける！
大学入試問題（数学）

第１１話　あなたの身近に『√２』君はいます！？

●第１話　むか〜し、むかしのことじゃった・・ 　ある日のこと、数学の先生が町を歩いていると一人の大工さんが頭をかかえて 　困っておりました。優しい数学の先生、心配になって声をかけてみると・・　 　先生：これこれ、大工さん、何をそんなに困った顔をしているのじゃ？？ 　大工：おお〜、これは数学の先生！　ちょうどよいところに来て下さった！　 　　　　実は王様から『面積が２平方メートルの正方形の入り口を作れ〜！！』 　　　　という仕事が入ったのです・・　気難しい王様のことですから少しでも 　　　　面積がちがっていると、私は牢屋に入れられてしまいます・・　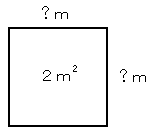 　　　　 　先生：それは困った王様じゃのう。 　大工：しかも私は計算があまり得意ではないのです・・ 　先生：ん〜、それは更に困ったことじゃなぁ・・。 　　　　よしよし、それでは私が一緒に考えてあげることにしよう！ 　大工：ありがとうございます！　　でも王様に説明するときに困っちゃいます 　　　　から、難しい計算は勘弁して下さいね・・ 　先生：ほっほっほっ、大丈夫、大丈夫！ ●数学の先生はこう考えました。 　先生：まずじゃな大工さん、面積が１平方メートルの入り口なら作れますな？ 　大工：はい、それならば楽勝です。メジャーで１メートルを測ればＯＫです。 　　　　私が困っているのは面積が２平方メートル・・ 　先生：まぁ、まぁ、慌てなさるな。それでは面積が１平方メートルの正方形を 　　　　２つ用意すれば２平方メートルになるではないか！ 　大工：先生〜、それじゃ長方形になっちゃうじゃないですか！？ 　先生：これこれ、まだ続きがあるのじゃ。最後までよくお聞きなさい。 　　　　　 　　　　この２つの正方形をじゃな、こうやって斜めに切っても全体の面積は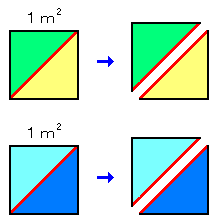？ 　　　　 　大工：切っただけですから変わりませんよ。２平方メートルです。 　先生：そうじゃな。そしたらこの４つの三角形をこうやってくっつけ直すと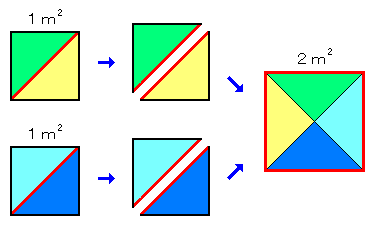？ 　　　　 　大工：おお〜！　面積が２平方メートルの正方形だぁ！！ 　先生：だから１辺が１メートルの正方形を書いて、その対角線の長さをひもで 　　　　測って、そのひもでまた正方形を作れば・・　ＯＫなんじゃな！ 　　　　１回も計算しないから、王様に説明してもこれなら大丈夫じゃ！ 　大工：ありがとうございます！！　さっそく工事に取りかかります！！ 　　　　それではまた〜！！ 　先生：あっ、おいおい、まだ最後のまとめがあったのに・・ 　　　　せっかちなヤツじゃのぉ・・　まっいっか・・ 　　　　ここまでこのお話を読んでくれた画面の向こうの君！ 　　　　そうそう、今これを読んでいてくれる、君じゃよ君！ 　　　　君はもう気がついていると思うが、この１辺の長さが「１」の正方形の 　　　　対角線の長さは、２乗したときに２（平方メートル）になる！　つまり 　　　　　　　　２乗したときに「２」になる元の数 　　　　と言う意味で『　√２（ルート）　』と書くんじゃったな！ 　　　　「ルート」っていうのは「元」ってことなんだな、これが。 　　　　おぉ〜、わしもそろそろ仕事にいくことにしよう。それじゃまたな！ 　　　　　　　　　　　　　　　　　　　　　　　　　（第１話　おしまい） ●　作図してみよう！　● 　面積が２００ｃｍ$2$の正方形をコンパスと定規だけで書いて下さい。 ●第２話　どっちが長い？？ 　さて、次の質問に一発直感で答えてみて下さい。どちらが長いでしょう？？　 ●　直感で答えてね！　● 　　学校でもらったプリント（わら半紙）を１枚用意して下さい。　　 　（１）短い方の辺を長い方の辺に合わさるように折って下さい。　　 　（２）すると図のような折れ線ができますね。　　　　　　　　　　 　　さて『長い方の辺』と『折れ線』ではどちらが長いでしょう？　　 ●重ねてみればどっちが長いか分かりますね！ 　答え合わせは簡単にできますよね！？ 　長い方の辺をクルッと曲げて折れ線に重ねてみて下さい。 　ぴったりと重なりましたよね！　つまりこの２辺の長さは全く同じなのです。 ●なぜ同じ長さになっているかというと・・・ 　それでは、なぜ同じ長さになっているのでしょう？ 　まず、「短い方の辺」と「長い方の辺」の長さについて考えてみましょう。 　短い方の辺の長さを「１」としましょう。長い方の辺は先ほどの折れ線と同じ 　長さでしたね。そこで下の図のように補助線を引いて正方形で考えてみます。 　１辺の長さが「１」の正方形の対角線の長さは、先ほどの第１話であったよう 　に「√２」となりますね。ということは長い方の辺の長さも√２になります。 　つまり・・ 　　　　　　　（短い方の辺）：（長い方の辺）＝１：√２ 　になっています。 　このことは大きなわら半紙でも小さなわら半紙でも全く同じになっています。 　それでは、なぜこんな比になっているのでしょうか？？ ●なぜ同じ長さになっているかというと・・・ 　それは、半分に切ったときに同じ形になるようになっているからなのです。　 　そのことを今のわら半紙で計算して確かめてみましょう。 （１）先ほどのようにわら半紙の短い方の辺の長さを「１」とします。 （２）長い方の辺の長さをいくつにしたら、半分に切ったときにその形が変わ 　　　らないか？が問題ですので、長い方の辺を「χ」とします。 （３）下の図のように半分に切った長方形で考えると、長い方の辺は「１」、 　　　短い方の辺は「χ／２」となりますね。 （４）この２つの長方形が同じ形（専門用語で『合同』ですね）になっている 　　　とすると、辺の比が等しくなりますから・・ 　　　　　１　：　χ　＝　χ／２　：　１ （５）比で書かれた式は「内項の積」と「外項の積」が等しくなりますから　 　　　　　１　：　χ　＝　χ／２　：　１ 　　　　　│　　　┃　　　　┃　　　　│ 　　　　　│　　　┗━━━━┛　　　　│ 　　　　　└─────────────┘ 　　　　　χ・χ／２　＝　１・１ 　　　　　χ$2$／２　＝　１ 　　　　　χ$2$　＝　２ 　ここで、　　χ　＝　±√２　となりますが、辺の長さは正ですから、 　　　　　　　χ　＝　√２　　となりますね！！ 　このような計算から、わら半紙など私たちの身の回りにある紙はその辺の比は 　１：√２　　となっています。（計算、ちゃんと分かったかな？？）

それでは、がんばって大学入試問題に挑戦してみましょう！ ここをクリックしてね。